

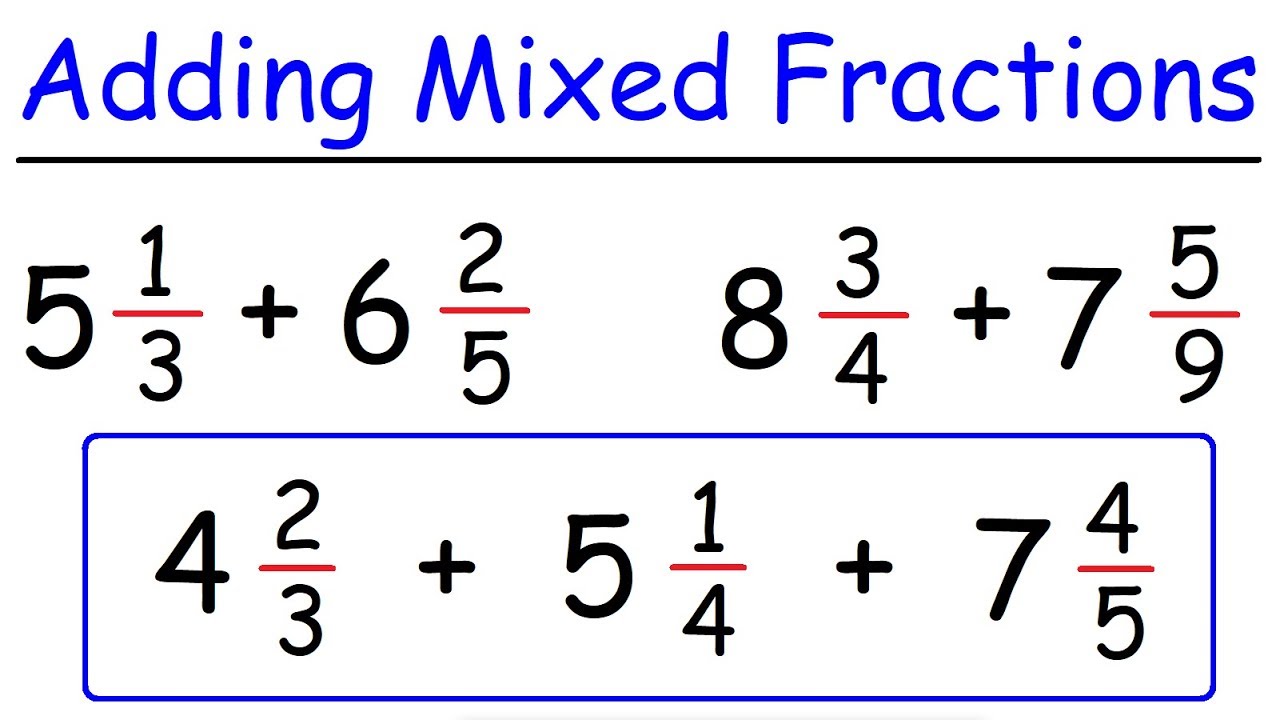
One, two, gets us to 5/6.While adding fractions the numerators are added and the denominator remains constant.
#ADD FRACTIONS PLUS#
Sixths, one, two, three, plus two of the sixths, And you can visualize it right over here. Plus two of that something, well it's going to beįive of that something. That everything is in terms of sixths, what is it going to be? Well it's going to be aĬertain number of sixths. And so this is the same thing as 3/6 plus this is going to be 2/6.

Instead of shading in just one of them, I now have shaded in two of them because that one thing that I shaded has now turned into two sections. That's what the denominator times two did. Of three equal sections, we now have six equal sections. So you multiply the numeratorĪnd the denominator by two. Took each of these sections and we made them into two sections. And to see why that makes sense, notice this shaded in gray part is exactly what we have here but now we I'd multiply the denominator by two but I'd also be That, it's one over three, I would want to take each of these thirds and make them into two sections. I want to add this to what? Well how do I expressġ/3 in terms of sixths? Well the way that I could do Thing as three over six and I want to add that or if And the green part which youĬould view as the numerator, I now have three times as many. Times as many divisions of the whole bar. So this, what we have in green, is exactly what we had before but now if I multiply it the numeratorĪnd the denominator by three, I've expressed it into sixths. The denominator by three and not change the value of the fraction, I have to multiply the It in terms of sixths, to go from halves to sixths, I would have to multiply So can we express 1/2 in terms of sixths and can we express 1/3 in terms of sixths? So we can just start with one over two and I made this little fractionīar a little bit longer 'cause you'll see why in a second. Use the least common multiple and the least common multiple And a good way to think about it is is there a multiple of two and three and it's simplest when you Now, what do we mean byĪ common denominator? Well what if we couldĮxpress this quantity and this quantity in terms So how do we do that? Well we try to set upĪ common denominator. Number of halves here and a certain number of halves here, well then we would know how
#ADD FRACTIONS HOW TO#
Things is we know how to add if we have the same denominator. So you could view this as this half plus this gray third here, what is that going to be equal to? Now one of the difficult And if you wanted to visualizeġ/3 it looks like that. So this is a visualization of 1/2 if you viewed this entire bar as whole, then we have shaded in half of it. You to pause this video and try to figure it out on your own. We're gonna try to figure out what 1/2 plus 1/3 is equal to.


 0 kommentar(er)
0 kommentar(er)
